MEMS resonators for real-time clocking applications

The work is carried out in the framework of the collaboration of the department of Civil and Environmental Engineering of Politecnico di Milano, Italy with STMicroelectronics.

People involved: V. Zega, A. Frangi

MEMS resonators for clock applications

Quartz crystals, thanks to their phase noise, thermal stability, ageing properties and power handling, were considered the frequency-reference industrial standard in the past century. Recently, MicroElectroMechanical Systems (MEMS) resonators entered the market of quartz oscillators as a possible solution to the increasing request of size reduction and integrability with the electronics and the other MEMS devices.

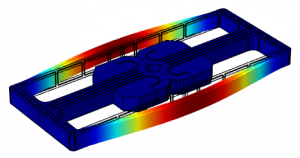
Figure 1: Modal analysis of a MEMS double-ended tuning fork resonator. The countour of the displacement field is shown in colour.

Thermal stability of MEMS resonators

Single-crystal silicon is a material with cubic symmetry and its stiffness matrix is defined by three elastic constants. If the Cartesian axes are aligned with the [100], [010] and [001] directions, it reads, for
T = 25 ◦C: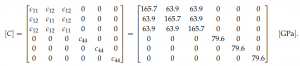

Once c11, c12 and c44 are computed for a given temperature and doping, the orientation of the mechanical structure with respect to the [100] direction is taken into account through a proper rotation applied to the stiffness matrix.

The temperature variation of the natural frequency of a MEMS tuning fork resonator is investigated in the reference temperature range [–35 ◦C–85 ◦C] and it is found that for each doping level there exists an intrinsic minimum for the frequency variation with temperature that decreases increasing the doping level. Moreover, it is possible to identify a proper orientation of the resonator such as the intrinsic minimum is reached for each doping level.

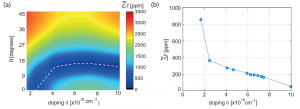
Figure 2: (a) Frequency variation in temperature for different orientations of the device with respect to the silicon wafer and for different n-dopings of the silicon. The white dotted line represents the minima of the contour plot. (b) Minimum temperature variation of the natural frequency of the resonator for different n-dopings of the silicon.

[1] V. Zega, A. Frangi, A. Guercilena, G. Gattere ‘Analysis of frequency stability and thermoelastic effects for slotted tuning fork MEMS resonators’ MDPI Sensors, 18(7) (2018) 2157.
[2] V. Zega, A. Frangi, A. Guercilena, G. Gattere ‘Numerical modelling of MEMS resonators’ ESMC 2018, Bologna, Italy, July 2-6, 2018

Optimization of MEMS resonators

Since it is possible to minimize the frequency variation with temperature by adjusting the orientation of the resonator with respect to the silicon wafer and the doping level, the next goal is to point-out a good strategy to maximize the quality factor of the MEMS resonator.

It is known from the literature that slots may significantly reduce the thermoelastic damping thus increasing the quality factor of the device.

An optimization procedure based on the evolutionary algorithm CMA-ES (Covariance Matrix Adaptation Evolution Strategy) has been applied for the determination of the geometry of the MEMS resonator that maximizes a suitably chosen multi-objective function accounting both for the quality factor and the frequency drift in temperature. Different constraints have been imposed to prove the versatility and generality of the proposed approach.

Nonlinear Dynamics of MEMS resonators

Numerical modelling of MicroElectroMechanical Systems (MEMS) resonators is attracting increasing interest from the sensors community especially when the nonlinear regime is activated by challenging applications of the device.
The dynamic response of a double-ended tuning fork MEMS resonator is studied both in the linear and nonlinear regime. A one Degree Of Freedom (1 dof) model able to predict the frequency response of the device is proposed. Geometric and electrostatic nonlinearities are simulated through a Finite Element Method (FEM) and a Boundary Element Method (BEM) code, respectively. The total damping of the resonator is computed by taking into account both the thermoelastic and the nonlinear fluid contributions. Experimental measurements performed on a resonator fabricated in polysilicon through a commercial surface micromachining process, validate the proposed model showing a very good agreement with theoretical predictions.

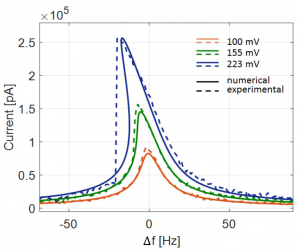
Figure 1: Frequency response of a DETF resonator. Numerical predictions and experimental measurements are reported in solid and dotted lines, respectively. The frequency responses correspond to a dc voltage of 3.6V on the mechanical structure and to different amplitudes of the time dependent signal on the driving electrodes: 100 mV, 155 mV and 223 mV. The pressure inside the package is assumed equal to 30 ubar.

[1] V. Zega, A. Frangi, G. Gattere, ‘Nonlinear Dynamics of MEMS resonators: numerical modelling and experiments’ IEEE Sensors 2019, Montreal, Canada, October 27-30, 2019.

Zega Valentina

Assistant Professor

Contacts