Close
Design and optimization of metamaterials
Optimization of auxetic materials
People involved: V. Zega, M. Bruggi, A. Corigliano
Complex inertial Micro Electro Mechanical Systems (MEMS) usually require the simultaneous motion of the masses in more than one direction and an overall linear behavior. Furthermore, since it is usually very difficult to actuate the device in all the required directions, complex spring configurations for the conversion of the motion are needed.
The goal of the work is to propose a new topology optimization procedure which can be used as a tool during the design phase of the optimal auxetic structure, that is completely compatible with the MEMS fabrication processes available so far and that allows the motion conversion in a MEMS device without entering the nonlinear regime. The most popular feature of auxetic materials or structures is the fact that they can expand in the direction perpendicular to an externally exerted tension, thus showing an equivalent negative Poisson’s ratio. Auxetic behavior is a scale-independent property which can be achieved at different structural levels from molecular to macroscopic levels.
First, auxetic configurations are found by performing the synthesis of compliant mechanisms, i.e. finding the distribution of material that maximizes a displacement component of the workpiece obtained as the output of the elastic response to an input represented by an imposed displacement applied elsewhere through an actuator. The main problem of this topology optimization procedure is the fact that the resultant auxetic structures have a truss-like shape and are, generally, too stiff for typical MEMS applications.
To solve this problem, a new formulation of topology optimization is implemented: it addresses the synthesis of compliant mechanisms using a Cosserat micro-polar material model instead of the Cauchy material model previously employed. The key point of the new procedure is that the constitutive law of a 2D micro-polar solid requires the introduction of a characteristic material length that governs the intrinsic material bending stiffness and that a suitable tuning of that characteristic length allows to generate optimal layouts whenever a bending-resistant design is preferred to a conventional truss-like solution.
Bibliography:
[1] M. Bruggi, V. Zega and A. Corigliano ‘Synthesis of auxetic structures using optimization of compliant mechanisms and a micropolar material model’ Structural and Multidisciplinary Optimization 55 (2017) 1-12
[2] V. Zega, M. Bruggi, A. Corigliano ‘Optimization of auxetic structures’ IV ECCOMAS young investigator conference, Milan, Italy, September 13-15, 2017
[3] M. Bruggi, V. Zega, A. Corigliano ‘Optimization of auxetic structures for MEMS applications’ Eurosime 2016, Montpellier, France, April 17-20, 2016
Deformation of the optimized auxetic structures
Schematic view of the auxetic structure obtained through the first topology optimization procedure in which a Cauchy elastic material is considered.
Schematic view of the auxetic structure obtained through the new topology optimization procedure in which a micro-polar Cosserat elastic material is considered.
Auxetic materials for vibrations insulation
People involved: V. Zega, L. D’Alessandro, R. Ardito, A. Corigliano
Auxeticity and phononic crystals bandgap properties are properly combined to obtain a single phase periodic structure with a tridimensional wide tunable bandgap.
When an external tensile load is applied to the structure, the auxetic unit cells change their configurations by exploiting the negative Poisson’s ratio and this results in the tuning, either hardening or softening, of the frequencies of the modes limiting the 3D bandgap.
Moreover, the expansion of the unit cell in all the directions, due to the auxeticity property, guarantees a fully 3D bandgap tunability of the proposed structure. Numerical simulations and analytical models are proposed to prove the claimed properties. The first experimental evidence of the tunability of a wide 3D bandgap is then shown thanks to the fabrication of a prototype by means of additive manufacturing.
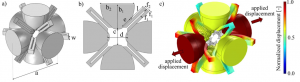
Figure 1: Unit cell topology. (a) 3D representation of the unit cell. (b) 2D cross section with respect to one of the principal planes. c) Auxetic (v ≈- 0.6) deformed shape of the unit cell computed by means of the Solid Mechanics Module of COMSOL Multiphysics v5.3. The contour of the displacement magnitude field is shown in color.
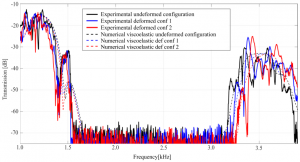
Figure 2: Tuning of the first bandgap: in solid lines the experimental results, in dashed lines the numerical visco-elastic model results.
Bibliography:
[1] L. D’Alessandro, V. Zega, R. Ardito, A. Corigliano ‘3D auxetic single material periodic structure with ultrawide tunable bandgap’ Scientific Reports 8:2262 (2018)
Emergent subharmonic band gaps in nonlinear locally resonant metamaterials induced by autoparametric resonance
People involved: V. Zega, P. B. Silva, M. G.D. Geers, V. Kouznetsova
High-performance locally resonant metamaterials represent the next frontier in materials technology due to their extraordinary properties obtained through materials design, enabling a variety of potential applications. The most exceptional feature of locally resonant metamaterials is the subwavelength size of their unit cells, which allows to overcome the limits in wave focusing, imaging and sound/vibration isolation. To respond to the fast evolution of these artifcial materials and the increasing need for advanced and exceptional properties, the emergence of a new mechanism for wave mitigation and control consisting in a nonlinear interaction between propagating and evanescent waves has recently been theoretically demonstrated.
A single-material nonlinear locally resonant metastructure (i.e. dimensions of the unit cell in the order of tens of mm) is designed, and for the frst time, the existence of the subharmonic attenuation zone induced by autoparametric resonance is experimentally proven. To the best of our knowledge, this represents the first experimental evidence of an emergent subharmonic band gap in a nonlinear locally resonant metamaterial.
To this aim, a locally resonant unit cell has been designed exhibiting predominantly quadratic nonlinear coupling between the host and the resonator, which, according to [1], is the prerequisite for promoting
the phenomenon under investigation. This has been achieved by exploiting the quadratic geometric nonlinearity arising in arched beams. Although the concept of arched resonators has been widely applied in micromechanical systems, to the best of our knowledge, this approach has not yet been used in a practical design of metamaterials that promote the quadratic non-linearity in a local resonator.
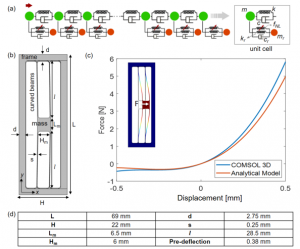
Figure 1. (a) 1D-discrete model presented in [1] for a nonlinear locally resonant metamaterial, (b) schematic view of the proposed resonant unit cell and (c) nonlinear force–displacement response of the resonator computed through an analytical single degree-of-freedom model and a 3D nonlinear static simulation in COMSOL Multiphysics. (d) Geometric dimensions of the unitcell of the proposed locally resonant metastructure. Te out-of-plane thickness of the unit cell (both frame and resonator) is 5 mm.
Numerical and analytical models are used to support the design process of the resonant unit cell, revealing an adequate agreement with the obtained experimental results.
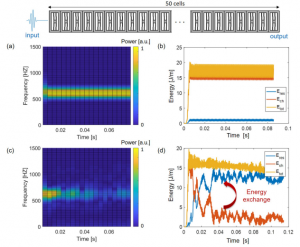
Figure 2. Spectrograms of the output signal computed at the right end of the chain. made of 50 cells in the (a) linear and (c) nonlinear regimes when a burst of 4 periods at around two times the frequency of the in-plane fexural mode of the resonator (i.e. 700 Hz) is applied on the lef side. The spectrograms are normalized with respect to the maximum power obtained in the linear regime. Te total energy (Etot) stored in the main chain (Ech) and in the resonators (Eres) is computed for the (b) linear and (d) nonlinear cases.
Bibliography:
[1] Silva, P. B. et al. ‘Emergent subharmonic band gaps in nonlinear locally resonant metamaterials induced by autoparametric resonance‘ Phys. Rev. E 99, (2019) 063003
[2] V. Zega, P. B. Silva, M. G. D. Geers, V. G. Kouznetsova ‘Experimental proof of emergent subharmonic attenuation zones in a nonlinear locally resonant metamaterial’ Scientific Reports, 10 (1), (2020) 12041.
Emergent subharmonic attenuation zones in nonlinear locally resonant metamaterials: numerical modeling and experiments
Summary of the work presented at ICTAM 2020+1 conference.
